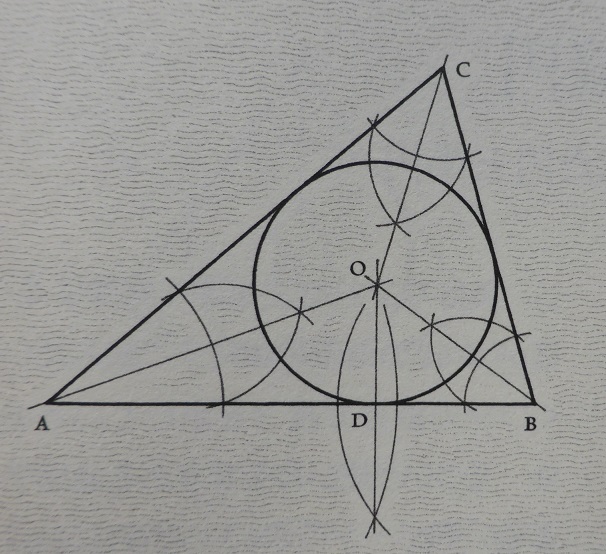
三角形の内接円の作図

１）それぞれの角の二等分線を作図
２）その交点が内心

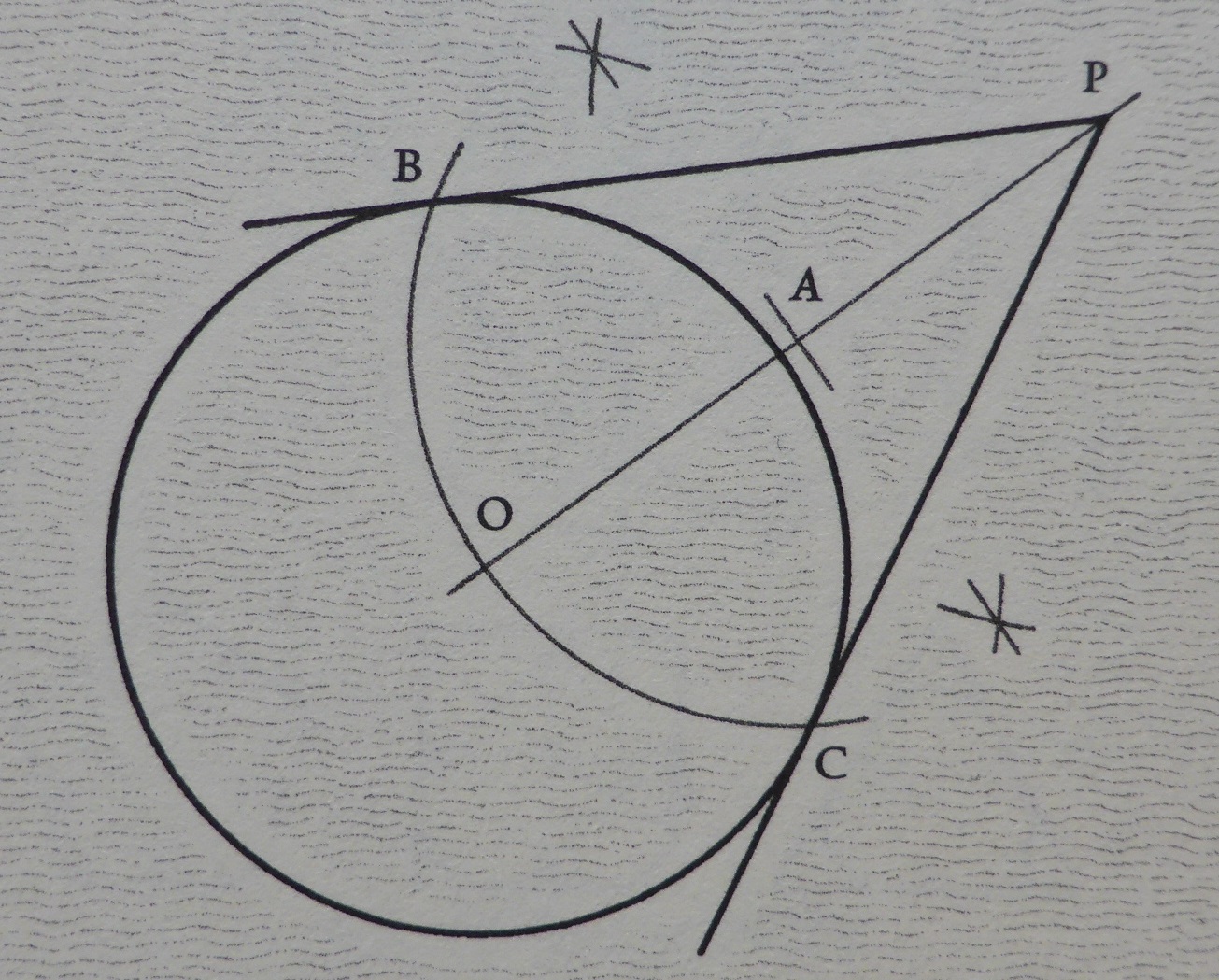円外の点からの接線

考え方　2点O-Pを直径とする円を考えると、円周角は直角になる。
１）OPの中点A
２）弧A-O（点B,C)　角OBPは90度の円周角
３）直線BP,CP

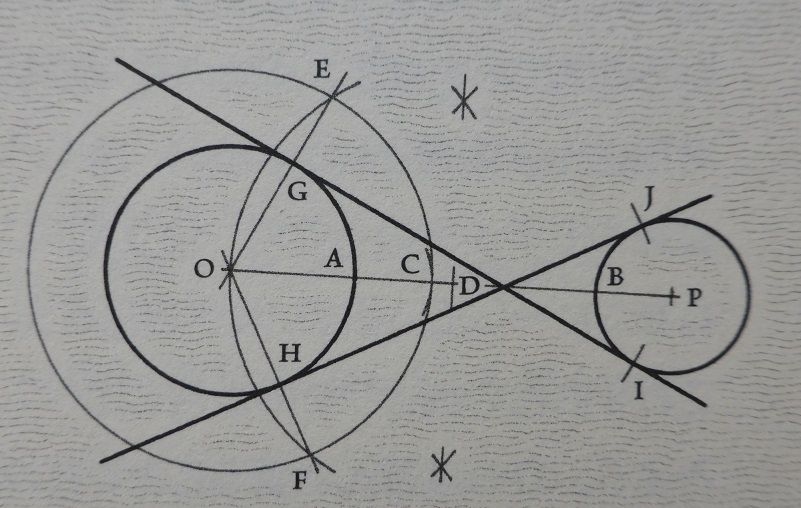
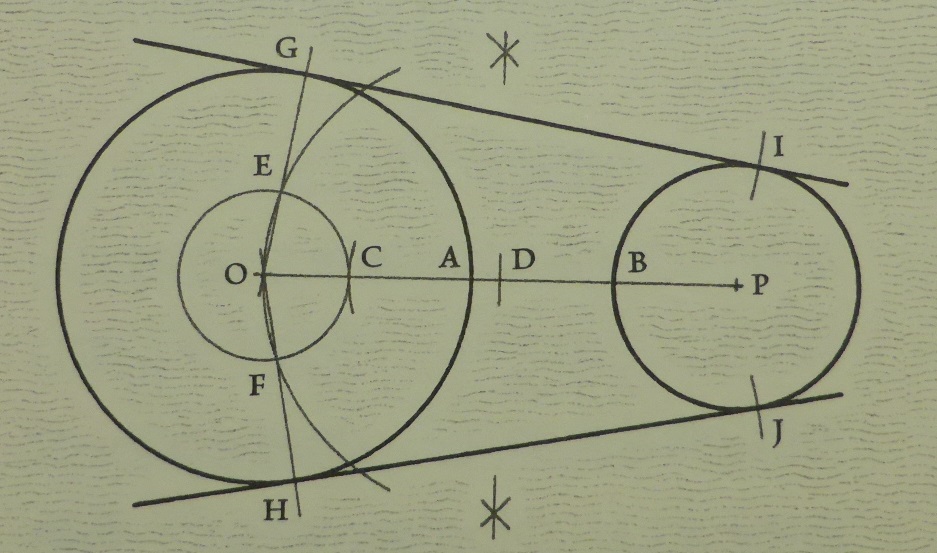
大きさが異なる２円の共通内接線の作図

考え方　２つの円の半径を足した円と、中心Pの接線を考える
　　　　その接線を右の円の円周まで平行移動する

１）直線OP（点A,B）
２）半径BP＋OA、中心Oの円
３）直線OPの中点D
４）弧D－O（点E,F）
５）直線OE,OF（点G,H）
６）直線EP,FP
７）半径EP＝FP、中心G,Hの弧（点I,J)
８）直線GI,HJ　　　　

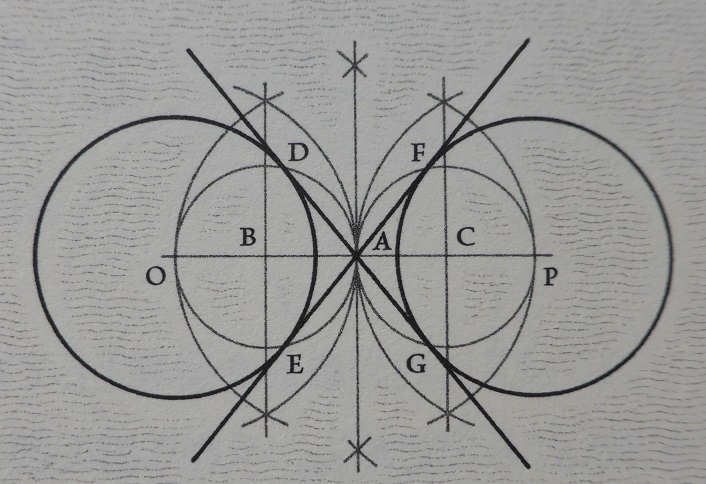同じ大きさの円も同様な作図で、共通内接線が作図できる

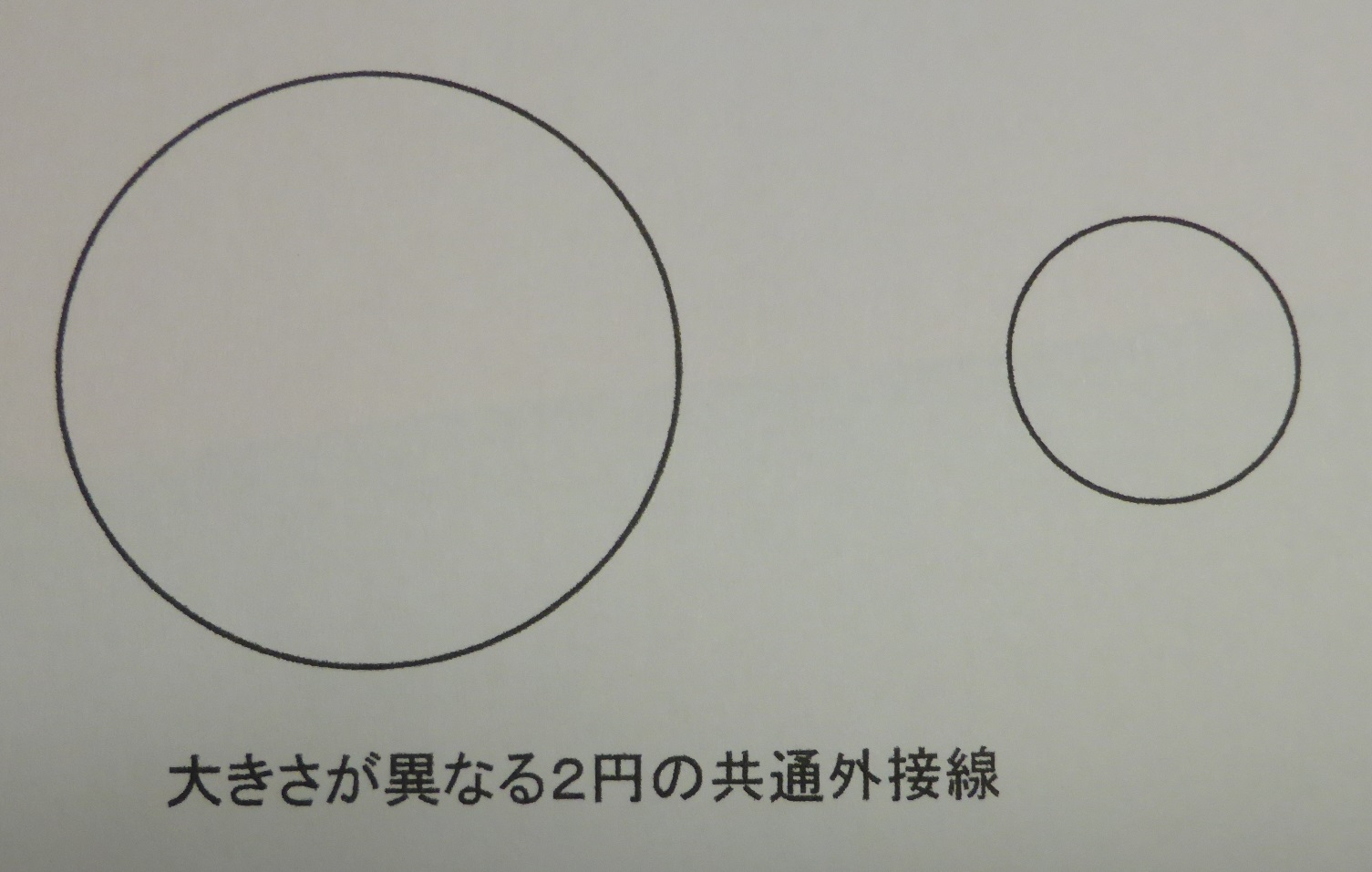大きさが異なる２円の共通外接線

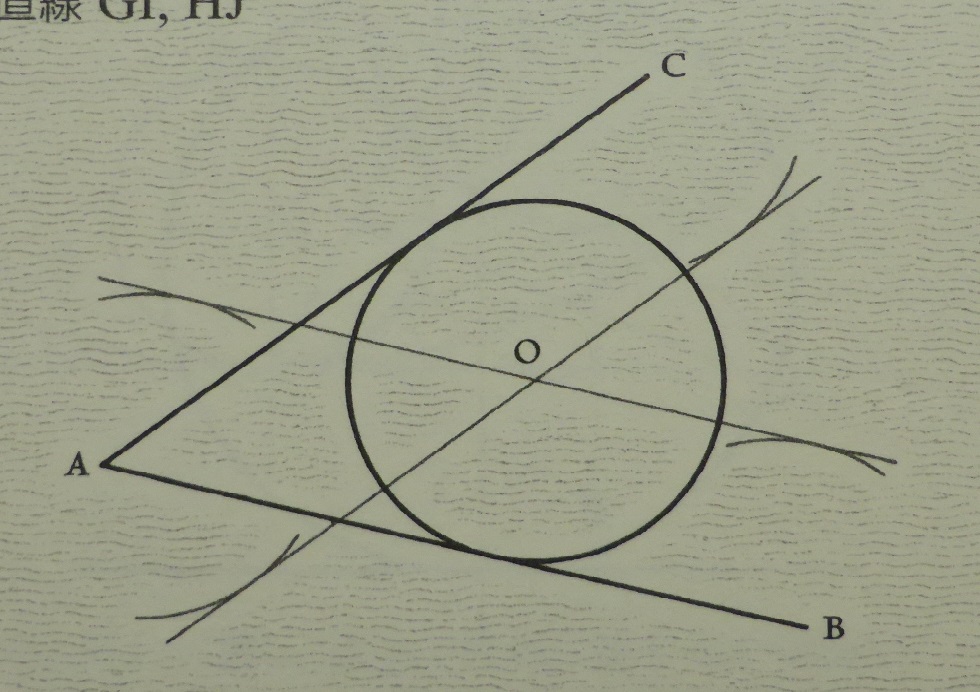
考え方　２円の半径の差を半径とする円を考える
その円と小円の中心を通る接線を引く


１）直線OP（点A,B)
２）半径PB,中心Aの弧（点C）
３）円O-C　
４）OPの中点D　　５）弧D-O（点E,F)
６）直線OE,OF（点G,H)　７）半径PE=PF、中心G,Hの弧（点I,J)
８）直線GI,HJ

２直線に接する、半径の与えられた円

考え方　半径の距離だけ離れた平行線


１）半径の距離だけ離れたAB,ACの平行線（交点O)
２）同じ半径、中心Oの円

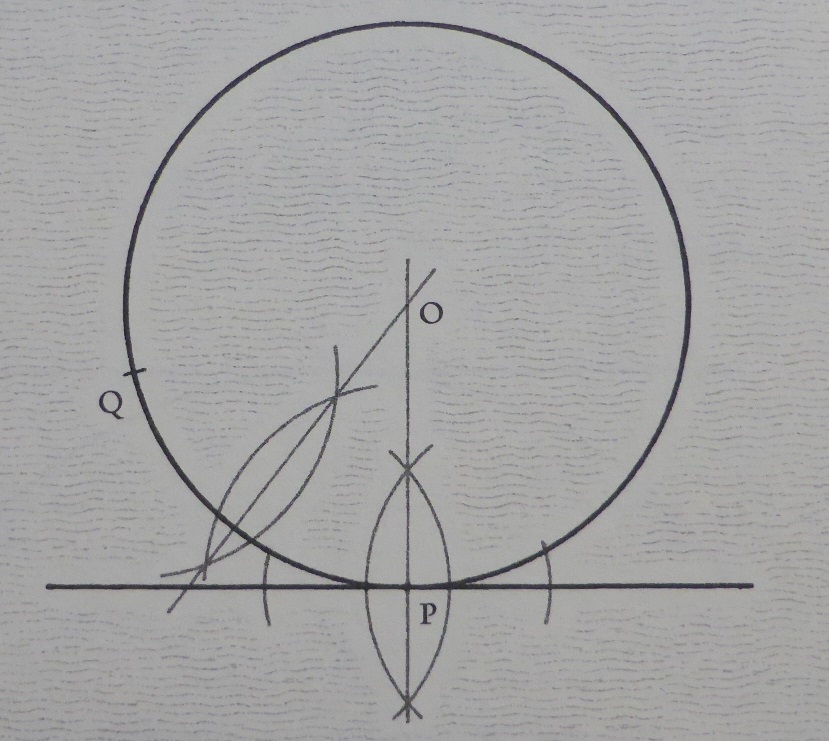
点Qを通り点Pで直線に接する円　の作図

考え方　弦PQの垂直二等分線と点Pを通る垂線の交点が円の中心

１）Pを通る垂線
２）PQの垂直二等分線（点O)
３）円O－PQ